[Science] Le codage RSA ou comment protéger vos transactions bancaires

Premier article Science and co. et ça va parler codage avec le système de codage RSA!

Je vais essayer de vous expliquer comment marche le système qui crypte la plupart des transactions bancaires, et ce système marche sur un principe assez simple mais très efficace, tout d'abord quelques rappels assez techniques...

(NB : Je n'ai pas détaillé les calculs pour éviter que ce soit trop fouillis, tous les calculs sont fait grâce à Maxima !).

De gauche à droite, Shamir, Rivest et Adleman, les trois inventeurs du système RSA.

Rappel 1: La division Euclidienne

Le premier rappel est un rappel de collège! Rappelez-vous de la division euclidienne, quand votre professeur vous demandait un calcul comme ceci:

Il vous demandait en fait d'écrire 119 = 11 x 10 + 9, où 9 est le reste de la division euclidienne de 119 par 11.
On peut en fait faire ce que l'on appelle des congruences grâce à la division euclidienne: que sont les congruences?
On écrit que A = B mod [p] si B est le reste de la division euclidienne de A par p.
Par exemple, 119 = 9 [11] (donc en gros, on fait la division euclidienne de 119 par 11 et on marque le reste après le signe égal) ou bien encore:

28 = 6 x 4 +4 (division euclidienne de 28 par 6 qui donne comme quotient 4 et comme reste 4) nous donne que 28 = 4 [6].

On peut voir le système de la division euclidienne comme un moyen de partager équitablement le maximum de bonbons entre un nombre donné de personnes. Par exemple, j'ai 28 bonbons à distribuer équitablement entre 6 personnes. 
Je leur donne d'abord à chacun un bonbon, il me reste 22 bonbons. Il m'en reste plus de 6 donc je redistribue à nouveau un bonbon à chacun. Il me reste 16 bonbons, donc toujours plus de 6, je continue. Je donne à nouveau un bonbon à chacun, ce qui me laisse 10 bonbons, je continue j'en redonne un à chacun. Il me reste 4 bonbons, je ne peux plus distribuer de bonbons à tout le monde (2 personnes n'en auront pas).
J'ai distribué 4  fois un bonbon à chacun, et lors d'une distribution, je donne 6 bonbons. Il me reste 4 bonbons. Donc on a que 28 (nombre de bonbons) = 4 (nombre de fois où j'ai distribué) x 6 (nombre de personnes) + 4 (nombre de bonbons qui me reste).
Donc 28 = 6 x 4 + 4.

En abrégé, grâce à l'écriture modulaire, ça donne 28 = 4 [6].

Le résumé de la distribution de bonbons :

Cliquer pour agrandir

À noter que si le reste de la division euclidienne d'un nombre par un autre vaut 0, on dit que le deuxième divise le premier.

Par exemple, en reprenant l'exemple des bonbons, on voit que si on disposte de 121 bonbons à distribuer entre 11 personnes, on pourra distribuer 11 fois un bonbon à chaque personne et il n'en reste plus à la fin.
Donc 121 = 11 x 11 + 0 (il ne me reste plus de bonbon).



Enfin, on dit qu'un nombre m est premier avec n si un nombre (différent de 1) qui divise n ne divise pas m et vice-versa. Par exemple, 9 est premier avec 2 car les diviseurs de 9 sont 1,3 et 9 et 3 ne divise pas 2, 9 non plus. Les nombres premiers entre eux représentent un certain intérêt en arithmétique.

Rappel 2: La factorisation en nombre premiers.

Un nombre premier, c'est un nombre premier qui n'est divisible que par 1 et par lui-même. Prenons un exemple précis:
Vous avez un certain nombre de bonbons, disons n bonbons. Vous devez les partager en part égale entre plusieurs personnes! Eh ben si le nombre n de bonbons est un nombre premier, vous ne pourrez diviser en part égale que si le nombre de personnes est 1 ou égal au nombre de bonbons!

Par exemple, vous avez 6 bonbons, vous pouvez les partager en 1 bonbon pour 6 personnes, 2 bonbons pour 3 personnes, 3 bonbons pour 2 personnes ou 6 bonbons pour une personnes.
Par contre, si vous avez 11 bonbons, vous ne pouvez les partager que de deux manières: soit vous en donnez 1 à 11 personnes ou 11 bonbons à une personnes. 11 est donc un nombre premier.
53 est un nombre premier également, et ainsi de suite...

Voilà une analogie pour vous présenter les nombres premiers... Et ces nombres premiers sont fascinants! Pourquoi donc ? Parce qu'ils constituent les briques des autres nombres, un peu comme les cellules qui font notre corps !

On a le résultat suivant qui nous dit qu'un nombre est factorisable de manière unique en produit de nombres premiers...

Encore un exemple: 198 = 2 x 3 x 3 x 11, et 2,3 et 11 sont des nombres premiers.

Le résultat dit qu'on peut le faire avec tous les nombres! Et c'est cela qui va nous intéresser...

Partie 1: La répartition des nombres premiers

Il faut savoir qu'on ne connaît pas la manière dont sont situés les nombres premiers dans la suite des nombres entiers, en connaissant un nombre premier on a aucun moyen de savoir actuellement où sera situé le prochain! Il peut être simplement deux nombres plus loin comme mille nombres plus loin... Et c'est ce qui rend les nombres premiers si intéressants! Ils vont constituer le coeur de l'algorithme RSA, le côté a priori aléatoire les rendant très durs à trouver...

Le codage RSA utilise des grands nombres premiers (de l'ordre de 2000 chiffres) pour pouvoir fonctionner. On prend donc p et q deux nombres premiers de 2000 chiffres et on écrit N = p x q. On peut donc dire que la factorisation en nombres premiers de N est p x q.

Partie 2: L'indicatrice d'Euler

Euler

C'est une fonction imaginée par Euler, je ne m’étendrai pas dessus, mais elle intervient plusieurs fois par la suite, on la note P(n), et elle compte en quelque sorte les nombres qui sont premiers avec n.

Retenez simplement que P(N) = (p-1)(q-1), où N = p x q, p et q sont deux nombres premiers.

Par exemple, si N = 5 x 7 = 35  , alors P(N) = (5-1)x(7-1) = 4 x 6 = 24. Il y a donc 24 nombres qui sont premiers avec N.

Partie 3 : Le petit théorème de Fermat.

De Fermat.

Un génial mathématicien Français du 17éme siècle, De Fermat, nous donna le théorème suivant qui est au centre du système de cryptage RSA.

Il nous dit que si p est un nombre premier et a un nombre entier qui n'est pas divisible par p (par exemple 8 n'est pas un multiple de 3, car on ne peut pas partager équitablement 8 bonbons entre trois personnes), alors on a que a^(p-1) = 1 [p], c'est-à-dire que le reste de la division euclidienne de a x a x a x ... x a (on multiplie a p-1 fois avec lui-même) par p est 1. Un exemple.

On prend p = 5, a = 3.
Alors a ^(p-1) = a^4 = 3^4 = 3 x 3 x 3 x 3 = 9 x 9  = 81.

La division euclidienne de 81 par 5 donne :
81 =  16 x 3 + 1.
Donc a^(p-1) = 3^4 = 1 [p].

Partie 4 : Comment ça marche ?

Nous y voilà ! Comment marche donc le système RSA ?

Il s'agît d'un code dit à clé asymétrique, c'est-à-dire que le public sait comment coder un message grâce au système RSA, mais le décoder, seule la personne qui a dit aux autres comment coder un message sait comment décoder.

A contrario d'un code symétrique : par exemple le code César qui consiste à décaler les lettres d'une place dans l'alphabet est symétrique car dès qu'une personne sait comment coder, elle sait comment le décoder.

Ainsi le message

"CPOKPVS" peut être facilement décrypter en "BONJOUR" et "BONJOUR" peut être facilement crypter en "CPOKPVS"

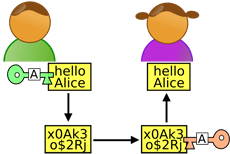
On peut résumer le système de cryptage à clé asymétrique grâce à cette image :

La clé qu'utilise le personnage vert est connue de tous alors que la clé qu'utilise Alice est connue d'elle seule.
Le personnage vert "ferme" le message et seule la clé d'Alice peut "ouvrir" le message.

Donc supposons que Roméo et Juliette veuillent s'envoyer des messages d'amour sans que personne soit au courant ! Juliette, connaissant le système de cryptage RSA, le met en place !

- Pour cela, elle va choisir deux (grands de préférence) nombres premiers, que l'on va noter p et q, ils vont rester secrets.

- Elle va ensuite calculer N = p x q (module de chiffrement).

- Juste après, elle va calculer P(N) = (p-1)x(q-1), l'indicatrice d'Euler de N.

- Elle choisit ensuite e un entier tel que e soit premier avec P(N) (basiquement, on peut essayer tous les entiers à partir de 2 pour tomber sur un entier premier avec P(N).

On va faire un exemple : 

Juliette choisit p = 7, q = 11. Donc N = p x q = 7 x 11 = 77.

P(N) = 6 x 10  = 60.

Il faut maintenant trouver un entier e tel que e et 60 soient premiers entre eux. 2 n'est pas premier avec P(N) car 2 divise 60, 3 divise 60 également, ainsi que 4, 5, 6. Mais 7 est premier avec 60 car 7  ne divise pas 60.

Posons e = 7. 

Ensuite, elle doit trouver le nombre d tel que, si l'on fait la division euclidienne du produit e x d par P(N), alors le reste est 1.

Ici, il faut donc trouver d tel que  7d = 1 [60]. Il existe des algorithmes sachant faire cela ! On va admettre que d = 43 "suffit". 

Maintenant, elle rend publique deux choses : les nombres N et e (tout le monde les connaît). Elle garde par contre secrets p, q, P(N) et d.

Pourquoi rendre public N ? Car il est difficile actuellement de trouver les nombres premiers p et q seulement à partir de N, si p et q sont très grands ! Donc on ne court pas beaucoup de risque en faisant cela. 

On se donne un entier M, plus petit que N, qui va jouer le rôle de Message.

Pour transmettre le message, Roméo doit calculer M x M x ... x M (M multiplié avec lui-même e fois) puis faire la division euclidienne de M par N pour trouver le message crypté et l'envoyer à Juliette.

Dans notre exemple, Roméo choisit M = 30, on calcule donc 30 x 30 x 30 x 30 x 30 x 30 x 30 = 21870000000. (30 multiplié 7 fois avec lui-même).

Puis on fait la division euclidienne de 21870000000 par N = 77.

Ça nous donne : 21870000000 = 77 x 284025974 + 2.

Donc on a que C = 2, ce qui sera le message que Roméo enverra à Juliette.

Juliette recevra donc C comme message, et contrairement aux autres, elle sait comment le déchiffrer :

Il lui suffira juste de calculer C^d (le fameux d qu'on a gardé secret)puis de faire la division euclidienne de C^d par N pour retrouver M.

Pour l'exemple, il faut calculer 2^43 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2= 8796093022208. Puis maintenant on fait la division euclidienne de 8796093022208 par 77, ce qui fait : 

8796093022208 = 77 x 114234974314  + 30.

Et on retrouve le message d'origine qui était 30.

Sans les nombres p,q,d et P(N), un individu qui intercepterait (en arrêtant le messager par exemple) le message C ne saurait pas immédiatement le décrypter, et les techniques mises en oeuvre actuellement pour décrypter sont clairement inefficaces car elles mettent très longtemps à donner un résultat (sauf coup de chance).

Bref, ceci est une brève introduction à un système qui sert encore grâce aux progrès des recherches en mathématiques et qui a été amélioré depuis.

D'autres systèmes se développent pour parer à toute découverte qui pourrait rendre obsolète le système RSA, donc ne vous inquiétez pas, vous pouvez dormir sur vos deux oreilles ! 

J'espère que vous l'aurez trouver clair, le sujet n'était pas d'un niveau facile mais j'ai essayé de vulgariser au maximum, n'hésitez pas à me faire un retour ! 

À bientôt pour un nouvel article Science & Co.